【學習筆記】資料結構－陣列

由於是個人的學習筆記，因此有可能存在錯誤，若有發現錯誤之處煩請糾正或者一起討論！

陣列(Array)

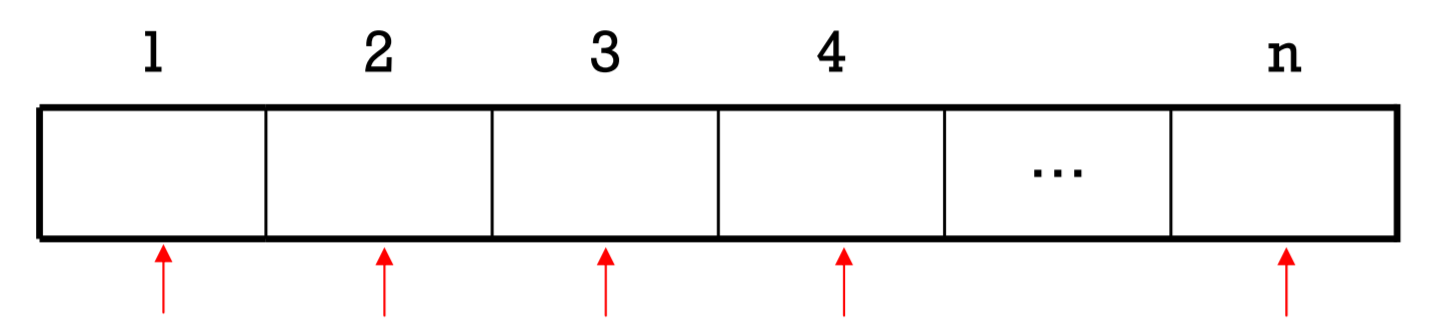
如果今天要計算全班20名同學的期中考英文成績總分，不使用陣列的話需要宣告20個變數(Score1,Score2…)，為了解決大批的資料處理，使用Array只需要宣告一個一維陣列來存放20名同學的英文成績，如Score[20]。

宣告陣列

下方是宣告陣列的程式碼

1 2	int[] arr; // arr is a reference to int[] arr = new int[4]; // 利用new指令產生物件

如果將陣列畫成圖就長這個樣子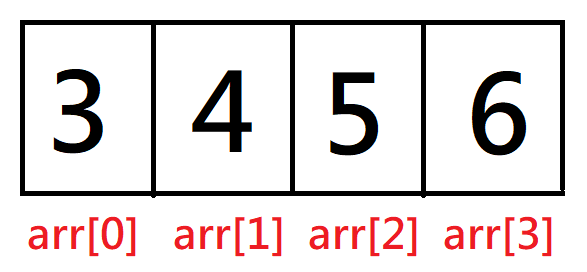

從圖中能看出，陣列是由陣列名稱[陣列索引]組成，arr[0]、arr[1]、arr[2]、arr[3]中的0,1,2,3便是索引(Index,也稱註標)，
陣列提供索引值(index)存取陣列中個別元素，每個索引值對應唯一一個陣列元素，因此我們只要指定陣列與索引值就可存取陣列中指定的元素。

而陣列又可分為一維陣列、二維陣列、多維陣列，你可以這樣宣告二維陣列

int arr[3][4] = {
    {1,2,3,4},
    {5,6,7,8},
    {9,0,1,2}
}

多維陣列也是以此類推，下圖是三維陣列的示意圖。

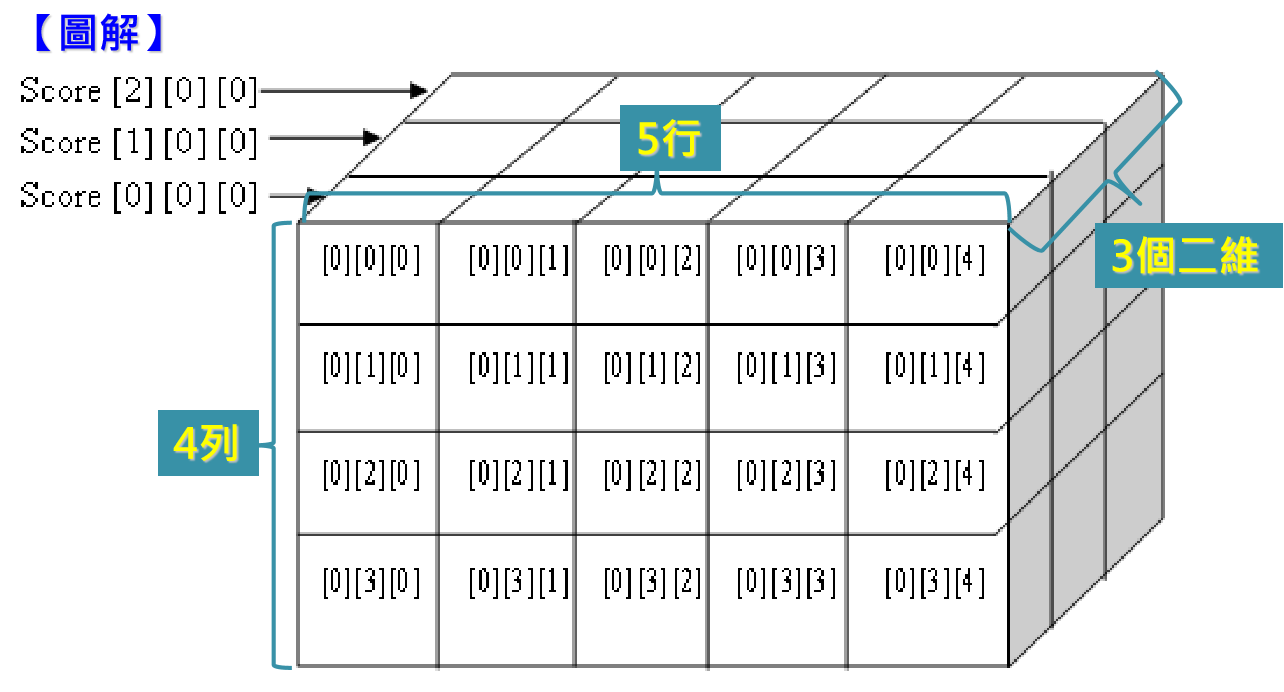
意思是宣告Score是由3個(0-2)二維陣列，每個二維陣列包含4列(0-3)，5行(0-4)組合而成的整數三維陣列。
並且共計有3×4×5＝60元素。

陣列特性

下面提提陣列的特性

為表示有序串列的一種方式
占用連續性的記憶體空間
各元素(Element)型態皆須相同
支援Sequential及Random Access
插入、刪除元素較為麻煩(因為需挪動其他元素)
Time = O(n)

假設今天我們需要插入一個元素

平均挪移次數 = (n+(n-1)+…+1)/n = n(n-1)/2 × 1/n = (n+1)/2 = O(n)

常使用的運算指令：

讀取(Read)
寫入(Write)
插入(Insert)
刪除(Delete)
複製(Copy)

讀取(Read)
利用索引(Index)來讀取

1 2	A={22,33,44,55} X=A[1]; // X=33

寫入(Write)
利用索引(Index)來寫入

1 2	A={22,33,44,55} A[1]=50; //A={22,50,44,55}

插入(Insert)
在指定的索引i的位置插入一項新元素，而原來索引i和之後的元素都必須往後挪一格。

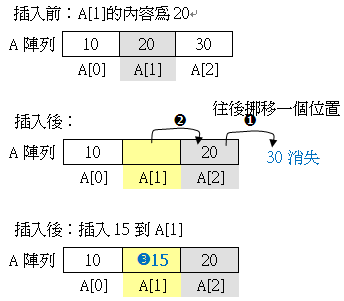
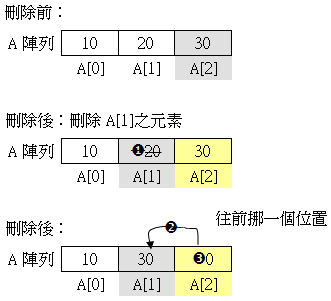
刪除(Delete)
刪除指定的註標i位置的元素，原來註標i的元素被刪除，為了避免浪費記憶體空間，因此之後的元素都必須要往前挪一個位置。(沒資料就補0)

複製(Copy)
將來源陣列的元素內含值全部逐一copy到目的陣列。

1 2	for(i=0;i<5;i++) B[i] = A[i];

陣列在記憶體中的儲存方式

計算Array中元素儲存位址

一維陣列

令：Lo為起始位址；d為元素大小, 則A[i]之位置計算 = Lo + i*d

Q：假設有個陣列起始位置A[0] = 100，d=2，則A[16] = ?

Ans：132

Q：假設有個陣列起始位置A[-3] = 100，d=1，則A[5] = ?
Ans：108

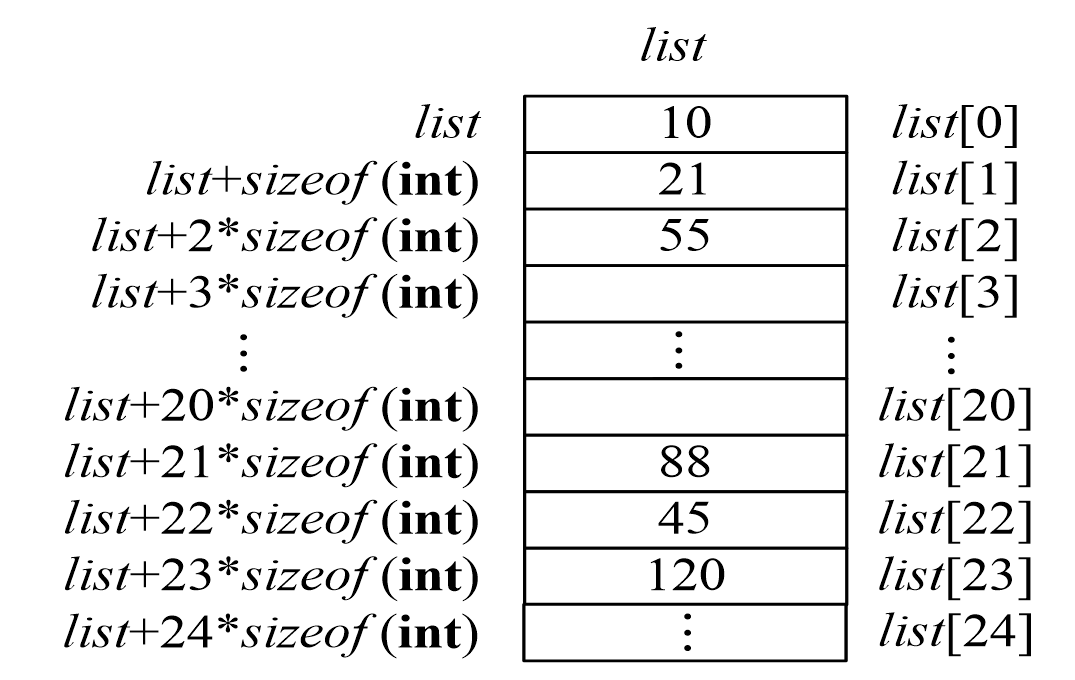
二維陣列

二維陣列分成以行為主(Column-Major)以及以列為主(Row-Major)。

以列為主
由上而下一列一列讀入一維陣列。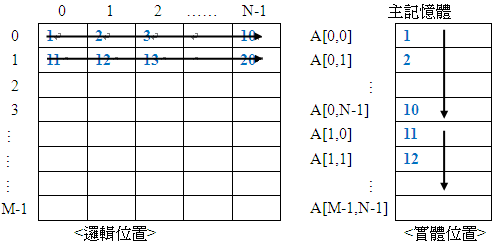

令Lo為起始位址
d為元素大小
則二維陣列A[i,j]位置會儲存到一維陣列的那一個位置呢？
公式：A[i,j] = Lo + (i * n + j) * d

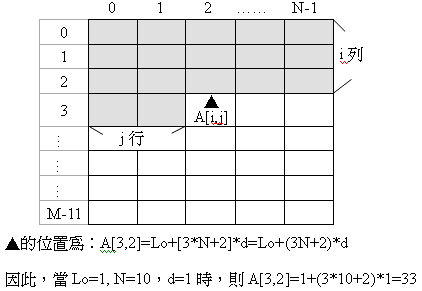
以行為主
由左往右一行一行讀入一維陣列。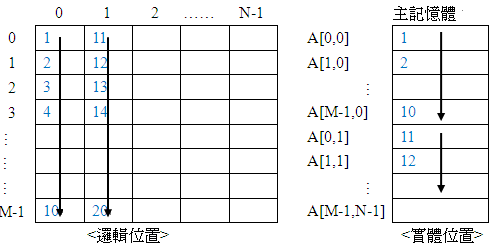

令Lo為起始位址
d為元素大小
則二維陣列A[i,j]位置會儲存到一維陣列的那一個位置呢？

公式：A[i,j] = Lo + (i + j * m )* d

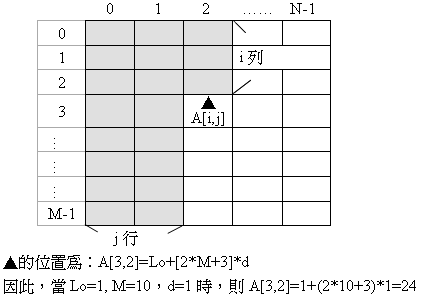
二維陣列所探討的二維陣列所探討的4個議題

給予所有宣告，求A[i, j]之位址

例: 若陣列A[5, 4]第一個元素為A[0, 0], Lo=1000，d=1，求A[3, 2]=? Ans：A[i, j] = 1000 + (3 × 4 + 2) × 1 = 1014

例：若陣列A[6, 5]第一個元素為A[1, 1], Lo=1000，d=1，求A[4, 3]=?
Ans：A[i,j] = 1000 + [(4 - 1) × 5 + (3 - 1)] × 1 = 1017

若陣列A[5, 4]第一個元素為A[0, 0], Lo=1000，d=1，求A[3, 2]=?
Ans：A[i,j] = 1000 + (3 + 2 × 6) × 1 = 1015

給予兩個已知位置，求A[i, j]之位址，須自行判斷出Row或Column-major

Row-Major時，列數較大的元素 ⇒ 位址必較大
Row-Major時，列數較小的元素 ⇒ 位址必較小
Column-Major時，行數大的元素 ⇒ 位址必較大
Column-Major時，行數小的元素 ⇒ 位址必較小

範例：令A[3, 5] = 14， A[5, 3] = 22
比較位址及列數：14 < 22, 3 < 5 ⇒ Row-Major

範例：令A[3, 5] = 14， A[5, 3] = 10
比較位址及行數：14 > 10, 5 > 3 ⇒ Column-Major

範例：令A[3, 5] = 14， A[5, 7] = 33
比較位址、列數、行數：14 < 30, 3 < 5, 5 < 7 ⇒ 無法判斷

範例：A[1, 1]的位址是2，A[2, 3]的位址為18，A[3, 2]的位址為28，求A[4, 5]的位址

首先判斷是Row-Major或Column-Major：
2 < 3, 3 > 2, 18 < 28 ⇒ Row-Major

因為A[1, 1] = 2 , ∴ Lo=2
代入公式A[i,j] = Lo + [(i-1)×n + (j-1)]×d，求出n和d
ａ[2, 3] = 2 + [(2-1)×n + (3-1)]×d = 2 + nd + 2d = 18 ⇒ nd + 2d = 16 — (1)
ａ[3, 2] = 2 + [(3-1)×n + (2-1)]×d = 2 + 2nd + d = 28 ⇒ 2nd + d = 26 — (2)

(1)×2 - (2) = 3d =6 ⇒ d=2, n=6

將A[4, 5] 代入公式A[i,j] = Lo + [(i-1)×n + (j-1)]×d
ａ[2, 3] = 2 + [(4-1)×6 + (5-1)]×2 = 46

給予兩個已知位置，但判斷出Row或Column-major皆有可能，求A[i, j]之位址

例: 若A[3,3]之位址為121, A[6,4]之位址為159,元素大小為 1, 求 A[4, 5]之位址.

先算Row-Major:
將A[3,3]與A[6,4]代入以下公式，求解Lo 與行數n:
A[i, j] = Lo +[(i-1)×n+ (j-1)] ×d
得: n = 37/3 (∵非整數, ∴ 不是Row-Major)

再算Column-Major:
將A[3,3]與A[6,4]代入以下公式，求解Lo 與行數n:
A[i, j] = Lo +[(i-1)+ (j-1) × m] ×d
得: n = 35, Lo = 49 (∵皆為整數, ∴ 是Column-Major)
得: A[4, 5] = 192.

給予三個已知位置量，求A[i, j]之位址

一定要假設元素大小 d (此時的元素大小不一定為 1)

當判斷出是Row-major或是Column-major時：

Row-major: 起始位置 Lo, n, d

Column-major: 起始位置 Lo, m, d

例：A(1, 1)之address為2，A(2, 3)為18，A(3, 2)為28，求A(4, 5)之位址?

Sol:
由 A(2, 3) 與 A(3, 2) 及其兩個位置，可以判斷出是Row-major (不要用A(1, 1)和另兩者之一比，會不好判斷!!)
此時，假設元素大小為 d，行數為 n

A(2, 3) = A(1, 1) + [(2-1)×n +(3-1)] × d
18 = 2 + nd +2d ………(1)

A(3, 2) = A(1, 1) + [(3-1)×n +(2-1)] × d
28 = 2 + 2nd +d ………(2)

因此， (1) ×2 - (2) => 8 = 2 + 3d，∴ d = 2。
再將 d 代回公式 (1)，可得 18 = 2 + 2n + 4，∴n = 6。
∴A(4, 5) = A(1, 1) + [(4-1) × 6 + (5-1)] × 2 = 46。

測驗

解答

1.陣列是一組變數的集合，而這些變數：

(A) 具有不同的資料型態，並且分散存在記憶體空間

(B) 具有相同的資料型態，並且分散存在記憶體空間

(D) 具有不同的資料型態，並且線性相鄰的存在記憶體空間

2.有關陣列下列那一項敘述有誤？

(A)佔用連續記憶體空間

(B)插入或刪除元素非常容易

©各元素的資料型態皆相同

(D)支援隨機存取(Random Access)與循序(Sequential Access)

3.存取陣列中的元素時，需指定要存取元素在陣列中的？

(A)記憶體位址

(B)索引編號

©元素值

(D)以上皆可

4.在一維陣列中，常使用的運算指令有五種，下列那一種不是？

(A)讀取(Read)

(B)寫入(Write)

©複製(Copy)

(D)貼上(Past)

5.在一維陣列中，那一個運算指令執行時，會往後挪一個位置？

(A)讀取(Read)

(B)寫入(Write)

©刪除(Delete)

(D)插入(Insert)

6.假設有n個整數利用陣列(Array)儲存，將存放於最前面及最後面的資料印出時，請問所需之時間複雜度以下列何者表示最為適當？

(A)O(1)

(B)O(log n)

©O(n)

(D)O(n^2)

7.假設有一陣列A儲存已排序的n個數字資料，刪除最大數值的資料需多少時間？

(A)O(1)

(B)O(log n)

©O(n)

(D)O(n^2)

8.假設有一陣列A儲存已排序好的資料(a1,a2,…,an)，請問下列何者錯誤？

(A)找第k大的資料需要O(log n)

(B)刪除需要O(n)的時間

©插入需要O(n)的時間

(D)以上皆非

9.請問在陣列中「讀取」某一元素的時間複雜度為何？

(A)O(1)

(B)O(log n)

©O(n)

(D)O(n^2)

7.請問在陣列中「寫入」某一元素的時間複雜度為何？

(A)O(1)

(B)O(log n)

©O(n)

(D)O(n2)

8.假設有一陣列A儲存已排序的n個數字資料，請問「插入」某一元素的時間複雜度為何？

(A)O(1)

(B)O(log n)

©O(n)

(D)O(n^2)

9.假設有一陣列A儲存已排序的n個數字資料，請問「刪除」某一元素的時間複雜度為何？

(A)O(1)

(B)O(log n)

©O(n)

(D)O(n^2)

10.假設有一陣列A陣列的元素內含值欲全部逐一複製到B陣列中，請問時間複雜度為何？

(A)O(1)

(B)O(log n)

©O(n)

(D)O(n^2)

11.關於「變數宣告」與「陣列宣告」的敘述，下列何者有誤？

(A) 變數宣告時，會產生不連續的記憶體空間的配置

(B) 變數宣告時，會產生連續的記憶體空間的配置

(D) 變數宣告時，變數與變數之間都是個別獨立的記憶體空間。

12.在陣列宣告時，如果宣告int A[10];，請問陣列註標的範圍為多少？

(A) A[0]、A[1]、A[2],…,A[10]

(B) A[0]、A[1]、A[2],…,A[9]

(D) A[1]、A[2],…,A[11]

13.有一整數陣列int A[0…29] ; （假設int資料型態佔用2個位元組），則此陣列共佔多少位元組？

(A) 40

(B) 30

(D) 60

14.陣列A[註標]中，註標不可為：

(A)整數

(B)運算式

©變數

(D)字串

答案：

CBBDD
AABAA
CCCBB
DD

陣列(Array)

宣告陣列

陣列特性

計算Array中元素儲存位址

一維陣列

二維陣列

測驗

參考資料