【學習筆記】資料結構導論

由於是個人的學習筆記，因此有可能存在錯誤，若有發現錯誤之處煩請糾正或者一起討論！

大綱

• 認識資料與資訊的關係
• 何謂資料結構(Data Structure)?
• 何謂演算法(Algorithm)?
• 程式設計概念
• 演算法的效率與評估

認識資料與資訊的關係

以下內容參考何謂資訊?何謂資料?其兩者關系為何? - 奇摩知識+

• 資料

1. 對於電腦的資料處理模式而言，未經處理而直接輸入電腦預備進行處理的數據稱為資料(Data)。
2. 通常資料指未知數據代表性的數據集合，亦即對事實的紀錄。
3. 資料依其特性亦可分為類比資料(例如溫度，聲波，色彩等)與數位資料(例如電壓)。

• 資訊

指經過電腦處理後，對資料輸入者而言，具有特定意義的資料集合。

因此：資料(Data) -> 經過處理與整理 -> 資訊(Information)。

例如今天有一份表格記錄著班級的期中考試成績，這些成績就是資料，而總成績、平均成績、排名則是資訊。這些資訊可以提供我們判斷及做決策的依據。

程式設計 = 資料結構 + 演算法

因此我們需要選擇適當的"資料結構"設計出最有效率的"演算法"，進而轉換成有效率的"程式"。

何謂資料結構(Data Structure)?

在電腦科學中，資料結構（英語：data structure）是電腦中儲存、組織資料的方式。 資料結構意味著介面或封裝：一個資料結構可被視為兩個函式之間的介面，或者是由資料類型聯合組成的儲存內容的存取方法封裝。 大多數資料結構都由數列、記錄、可辨識聯合、參照等基本類型構成。舉例而言，可為空的參照（nullable reference）是參照與可辨識聯合的結合體，而最簡單的鏈式結構連結串列則是由記錄與可空參照構成。 資料結構可透過程式語言所提供的資料類型、參照及其他操作加以實現。一個設計良好的資料結構，應該在儘可能使用較少的時間與空間資源的前提下，支援各種程式執行。 . . . －－－維基百科

太生澀難懂了！有沒有更簡潔有力一點的解釋？

資料結構就是在探討如何將資料有組織的存放在記憶體中，以提升程式 的執行效率。

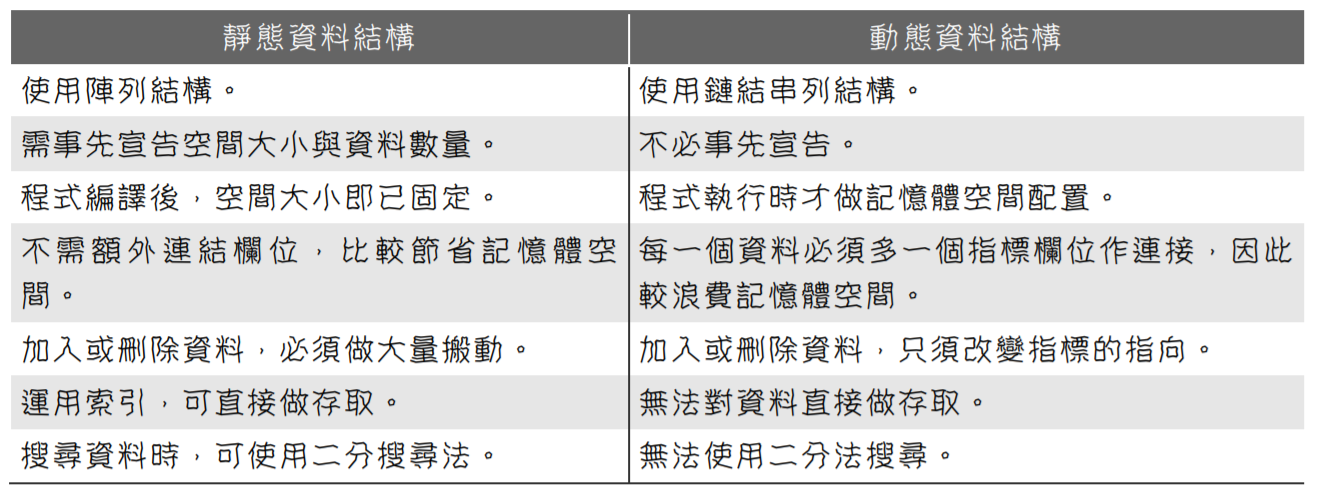
靜態與動態資料結構

1. 靜態(Static)資料結構：所謂靜態資料結構，是指資料所占用的空間大小及資料數目都必須事先宣告，因此在程式編譯的同時，空間的大小及資料數目就無法改變了。
2. 動態(Dynamic)資料結構：所謂動態資料結構，資料所使用之空間大小及資料數目都不必事先宣告，在程式執行時才做記憶體的空間配置。

陣列的使用就是靜態資料結構的代表，而動態資料結構則以鏈結串列結構為代表。

常見的資料結構

• 串列 (List): 先來先買，或稱序列 (sequence)
• 陣列 (Array)
• 堆疊 (Stack): 後進先出，又稱為棧或堆棧
• 佇列 (Queue)
• 樹狀結構 (Tree)
• 圖形結構 (Graph)

…等，不只這些，其他的以後再說。

串列(List)

分為循序串列(如:陣列)以及連結串列，連結串列之後再說。

陣列(Array)

1. 占用連續記憶體空間。
2. 用來表示有序串列之一種方式。
3. 各元素的資料型態皆相同。
4. 支援隨機存取與循序存取。
5. 插入或刪除元素時較為麻煩，因為需挪移其他元素。

下方就是宣告陣列的程式碼：

int[] data = new int[100]; //宣告陣列大小
data[0]  = 1; //陣列第一格存放的整數是1

堆疊(Stack)

1. 堆疊原理為後進先出(LIFO, Last In First Out)。
2. 只允許在最新的資料那端操作。
3. 加入資料稱為Push(推入)，移除資料稱為Pop(彈出)。

常與另一種有序的線性資料集合 佇列 相提並論。
堆疊常用 一維陣列 或 連結串列 來實現。

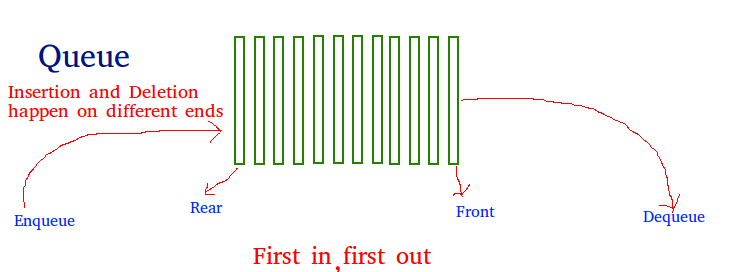
佇列(Queue)

1. 佇列原理為先進先出(FIFO, First-In-First-Out)。
2. 似堆疊，但佇列可以在兩端進行資料操作。
3. 佇列只能在後端(rear)插入操作，稱為進入佇列(Enqueue)；只能在前端(front)刪除資料，稱為輸出佇列(Dequeue)。

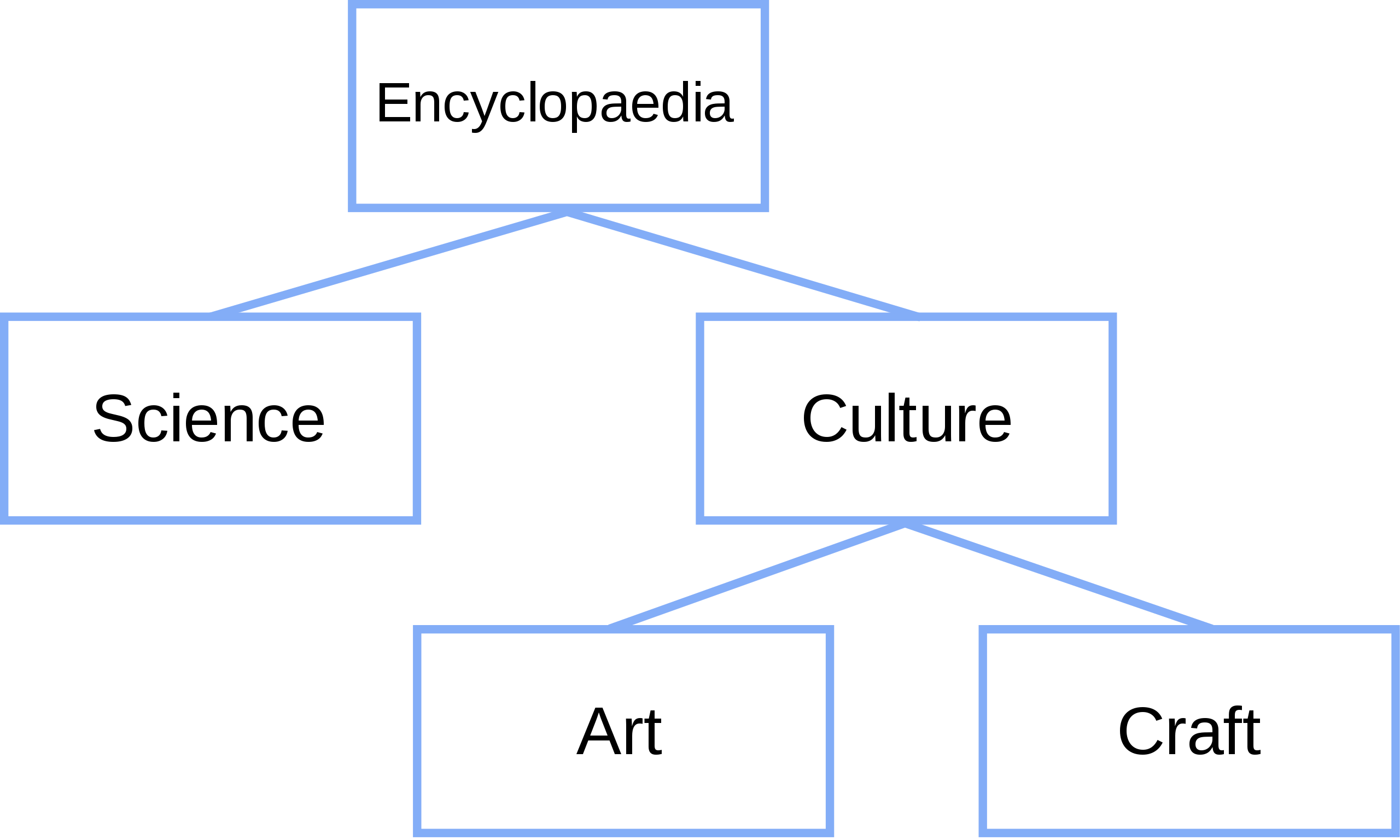
樹狀結構(Tree)

依照圖來看它是一個上下顛倒的樹，其根部在上方，是資料的開頭，而下方的資料稱為葉子。

圖形結構(Graph)

圖形很像樹狀結構，不同的地方是節點之間沒有父子關係。

請參考認識圖形結構

何謂演算法(Algorithm)?

用於有限步驟內解決一個特定問題。

例如：

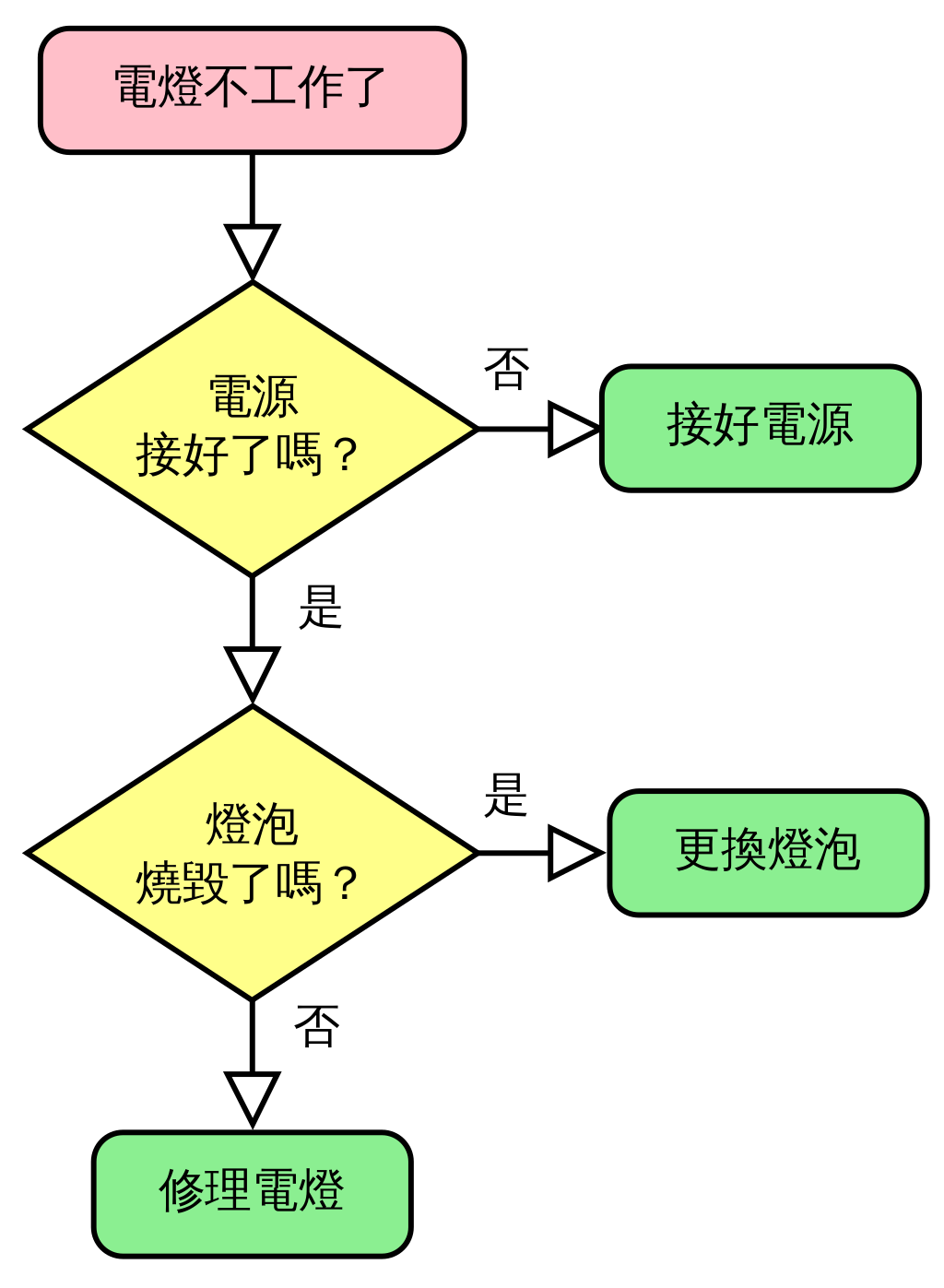
你可以稱之為「應對燈泡不亮的簡單演算法」。

演算法的特性

一個演算法需要俱備的五個特性：輸入(Input)、輸出(Output)、明確性(Definiteness)、有限性(Finiteness)、有效性(Effectiveness)
不一定要有輸入，但至少要有一個輸出。

明確性

每一行指令都必須明確，不可模稜兩可。

今天有一個情境，需要判斷某數值是否為偶數。

(1)輸入一個正整數
(2)作餘數運算是否為0
(3)為0即為偶數

從演算法觀點來看，第二點並不符合明確性，因為並無說明餘數運算是如何運算。

應該改寫成：

(1)輸入一個正整數N
(2)除果N除以為其餘數為0
(3)則其N為偶數

有限性

演算法必須能終止執行，亦即必須在有限的步驟內完成。

必須說的是：真正的程式是可以有無窮迴路的動作，但演算法並非是真正可以執行的程式。

例如：Windows作業系統除非系統關機或當機，否則它會永遠執行「等待迴圈」，等待使用者從輸入設備輸入指令。

有效性

演算法的處理動作必須是有效且具體可行的，同時能讓使用者使用紙筆計算獲得答案。

因此，演算法是一個演算法是明確、有效、最終會結束的可執行步驟。

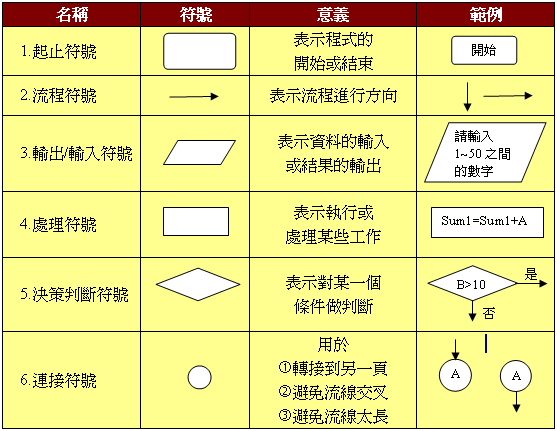
描述演算法的方法

描述演算法的方法有：

1. 文字描述
2. 流程圖(Flow Chart)
3. 虛擬碼(Pseudo Code)
4. 電子電路
5. 數學
   …等

流程圖

利用「流程圖」來描述使用者登入帳號與密碼時，系統檢查的過程。

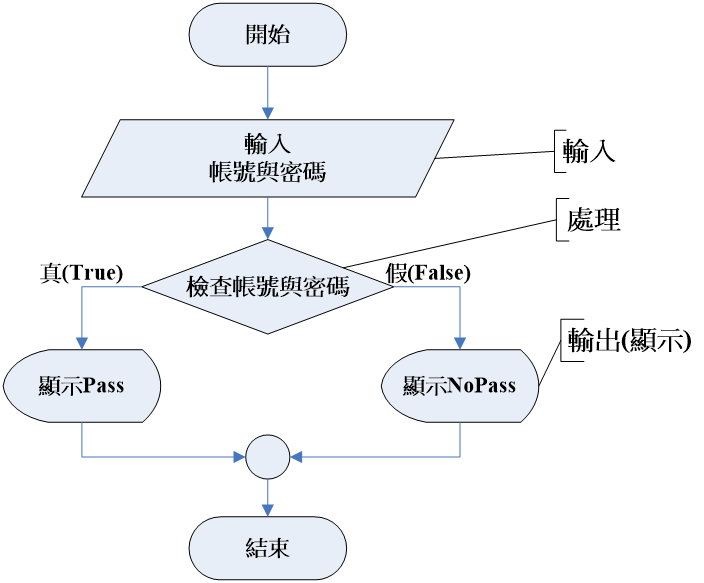
虛擬碼

兼具文字描述及流程圖的優點，其方式是用文字摻雜程式語言，來描述解題步驟與方法。

Input: UserName,Password
IF(UserName and Password) ALL True
Output: You Can Pass!
else
Output: You Can't Pass!

資料結構中一般都是利用虛擬碼(Pseudo Code)來表示演算法。

演算法的基本結構

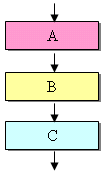
循序 (Sequence) 結構
依先後順序，一個步驟接著一個步驟依序執行。

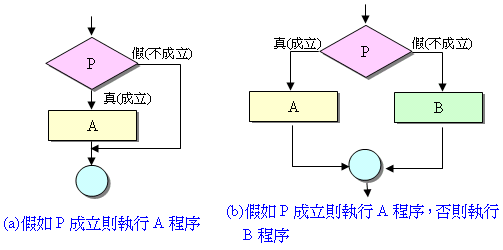
選擇 (Selection) 結構
依據不同的條件，選擇不同的解題步驟執行。

重複 (Iteration) 結構
部分解題步驟需要反覆執行，直到符合或是不符合某一條件式時，才會離開重複執行的部份。
重複結構也常被稱為「迴圈 (Loop)」 。

程式設計概念

1. 分析所要解決的問題(需求)

2. 設計解題的步驟(演算法)
   例如Binary Search(二分搜索算法)

3. 編寫程式(程式碼)

4. 上機測試,偵測錯誤(debug)

Programming Language Error:

(1)Syntax Error(語法錯) - 只在編譯時出現(Compiler Time)

例如以下的程式是正確的：

System.out.println("Hello World");

以下的程式不正確：

System.out.println(Hello World);

第二個程式理論上要顯示的是叫作Hello World的變數，而不是Hello World這個字，且Java語言的變數名稱中不可有空白，因此會出現語法錯誤。

(2)Semantic Error(語意錯) - Logical Error

程式語法雖然正確但無法提供正確的功能。

例如用C語言計算平均數，以下程式雖然能夠通過編譯並執行，但結果是錯誤的。

int average(int a, int b)
{
    return a + b / 2;     /* 應為 (a + b) / 2 */
}

Debug methods:
(1) Single steps
(2) Breaking Point Setting

5. 編寫程式說明書(可執行)

演算法 VS 程式
演算法是以人為主，任何人都可以閱讀的程式碼，強調「可讀性」。
程式是以電腦為主，強調執行結果正確性(Correctness)、可維護性(Maintainable)及執行效率(Performance)。

演算法的效率評估

評估演算法的三種方法：

1. 最差狀況分析(Worst-case analysis) [最廣用]
   在所有可能的輸入組合下最多所需要的時間(Upper bound)，O(n)最常被使用來表示理論「上限」。

2. 平均狀況分析(Average-case analysis)
   在所有可能的輸入組合下平均所需時間(Average Time)。

3. 最佳狀況分析(Best-case analysis)
   分析演算法對何種輸入資料所需花費的時間最少(Lower bound)。

基本上時間複雜度的分析比空間複雜度來的重要，因為當資料量龐大時，時間複雜度會有較大的差異性，空間複雜度則差異較小，再加上目前的記憶體相當便宜，因此目前在資料結構所探討演算法之效率評估，都著重在時間複雜度方面。

1.時間複雜度(Time Complexity)

定義：演算法執行時，所需花費的時間。
分析方法：統計演算法中指令執行的次數。(演算法有多快不是以秒衡量，而是以步驟次數。)

註解、括號、函式宣告及變數宣告不列入執行時間計算。
變數宣告時若有指派初始值，則視為1次。
函式呼叫視為1次。
不考慮指令本身的複雜度或實際執行時間，一個指令皆視為1次。

範例：

//假設某電腦執行加法要5微秒，減法要10微秒，乘法要20微秒。
不管實際執行時間A=0、A++、A--、A=A*5都視為執行一次。

範例：

int sum(int[] data)                     // 0次
{                                       // 0次
    int i;                              // 0次
    int sum = 0;                        // 1次

    //for迴圈最後會判斷條件不成立，跳離迴圈，所以比其內容多執行一次
    for(i = 0; i < data.length; i++){   // data.length+1次
        sum += data[i];                 // data.length次
    }                                   // 0次
    return sum;                         // 1次
}

時間複雜度常用大O符號表述一個演算法在輸入 n 個東西時，總執行時間與 n 的關係。

時間複雜度的公式是： T(n) = O( f(n) )，其中f(n) 表示每行代碼執行次數之和，這個公式的全稱是：算法的漸進時間複雜度。

如果一個演算法對於任何大小為ｎ（必須比n0大）的輸入，它至多需要 5n^3 + 3n的時間執行完畢，那麼它的漸近時間複雜度是 O(n^3)。

取執行次數中最高次方或最大指數部分

O(1)

function(int n){
    print(n); # 1 次
}

O(n)

function(int n){
    for(i=0; i<n ;i++){ # n+1 次
        print(i); #輸入的 n 的數量會跑 n 次
    }
}

O(n²)

function(int n){
    for(i=0; i<n; i++){ # n+1 次
        for(j=0; j<n ;j++){ # n*(n-1) 次
            print(i * j); #n²次
        }
    }
}

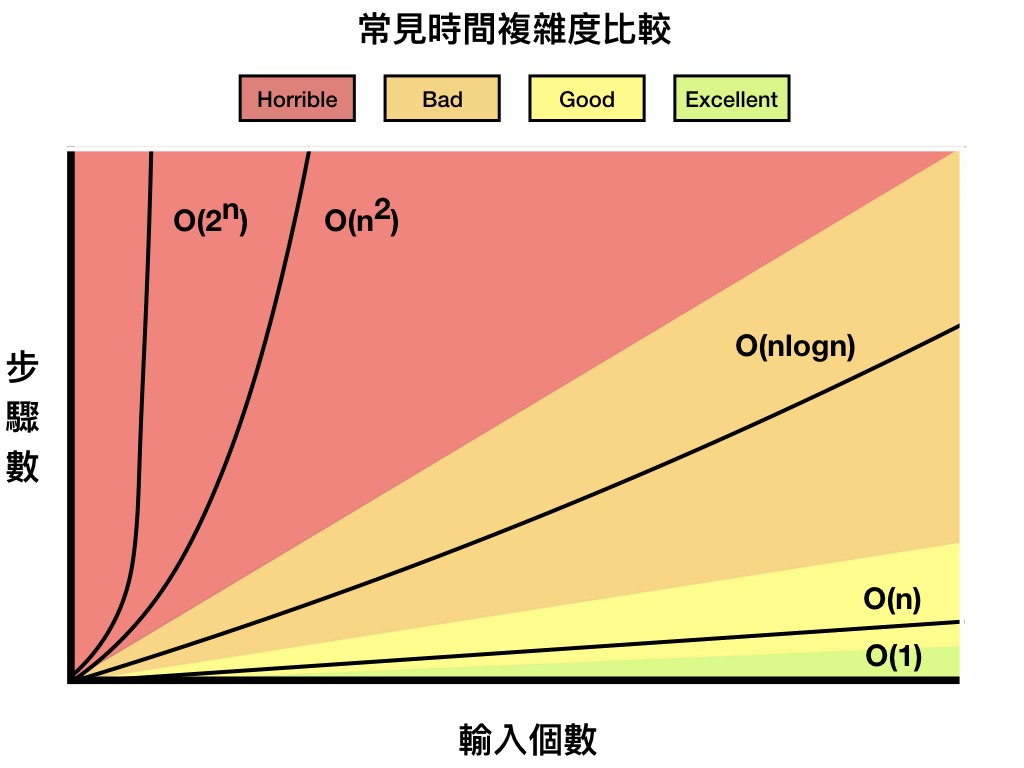
常見的六種時間複雜度與演算法
O(1)：陣列讀取
O(n)：簡易搜尋
O(log n)：二分搜尋
O(nlogn)：合併排序
O(n²)：選擇排序
O(2^n)：費波那契數列

時間複雜度的比較

2.空間複雜度(Space Complexity)

定義：演算法執行時，所需花費的記憶體。

分析方法：統計演算法中所使用的固定空間(Fixed Space)和變動空間(Variable Space)。

固定空間(Fixed Space, C)：非主要考量

• 程式碼大小(Instruction Space)
• 簡單變數(EX：int, float,…)
• 常數
• 固定大小的結構變數(EX：陣列、記錄、…等）

變動空間(Variable Space, SP )

• 參數：以傳值呼叫(Call By Value)傳遞的參數(EX：陣列)
• 遞迴所需的堆疊空間

固定空間通常都是必要的，所以當有使用空間限制的需求時，只會考慮能否節省變動空間。
空間函式S(P)：表示當輸入資料量為n時，演算法中指令所需執行的次數。
格式：S(P) = C + SP

參考：[資料結構] 演算法評估與資料型別

O(1)
不會影響使用的變數數量。

function(int n){
    for(int i=0;i<n;i++){
        print(i);
    }
}

O(n)
會隨著丟進去的數字而影響變數的量。

function(int n){
    int c[n];
    for(int i=0;i<n;i++){
        c[i] = i;
    }
}

參考資料

《演算法圖鑑》第一章：資料結構
演算法的表示–流程圖
【演算法】入門介紹－什麼是演算法 What’s Algorithm?
初學者學演算法｜從時間複雜度認識常見演算法（一）
資料結構筆記(一)：演算法、時間複雜度、空間複雜度
初學者學演算法｜談什麼是演算法和時間複雜度
Second Round 目錄：演算法與資料結構
程式語言的控制結構
[資料結構] 演算法評估與資料型別
算法的时间与空间复杂度（一看就懂）
基礎電腦科學：演算法概要